Контрольный листок, 2014, № 9
Против ЕГЭ
Итоги ЕГЭ: опыт анализа
© Люция Нуриева, Сергей Киселев
Накануне 2013 года Президент РФ подписал закон «Об образовании», видимо поставившего точку в затянувшихся спорах «быть или не быть» Единому государственному экзамену. С неоднозначными результатами экзамен всё же состоялся.
«Настал важный момент, когда должен произойти процесс нормальной "приватизации” результатов ЕГЭ субъектами Российской Федерации, — заявила в одном из интервью руководитель (теперь уже бывший) Рособрнадзора Л. Глебова. — Пришло время задуматься над тем, что делать с результатами с точки зрения анализа итогов госэкзамена».
Действительно, как показывает десятилетний опыт проекта, итоги ЕГЭ нуждаются в критическом осмыслении и инвентаризации. Отсутствие своевременного анализа ведет к консервации застарелых ошибок и запоздалому реагированию на появление новых проблем, что оборачивается против самого экзамена и его участников. В нашей статье мы хотим обратить внимание на конкретную практику проведения испытаний и подведения итогов, недостатки которых могут быть устранены.
Технология измерений
Одним из самых уязвимых мест в тестовой технологии измерений уровня знаний являются закрытые вопросы, позволяющие угадывать ответы. Большую часть работы на ЕГЭ составляют задания закрытого типа с 4 альтернативами выбора (в иностранном языке — с тремя). Их доля в первичном балле по истории и обществознанию составляет почти 40%, по русскому языку, биологии, физике и химии — около 50%. Более того, вопросы с кратким ответом (обычно часть В) в основном тоже закрытые, хотя и предусматривают множественный выбор. Действительно открытых вопросов в контрольно-измерительных материалах (КИМ) по всем предметам очень мало (как правило, только в части С).
Алгоритм выполнения заданий части А — это последовательный просмотр и отсев сомнительных вариантов ответа. Общий недостаток закрытых вопросов — подсказка в альтернативах. Дело даже не в том, что некоторые из них сразу видны как верные. Общим правилом является то, что большинство неверных альтернатив откровенно неправдоподобно. Исключая их, можно получить верный ответ, даже не зная его.
Технология выполнения части А по физике и информатике (где требуются вычисления) максимально приближена к обычной письменной работе. Однако и здесь присутствует элемент подсказки. Закрытый вопрос позволяет сравнивать полученный ответ с предложенными вариантами. Если совпадений нет, то задача решается до достижения успеха. Открытый вопрос сигнала для повторного поиска верного ответа уже не давал бы. При затруднении подходящий вариант выбирается приблизительно. И в любом случае сохраняется 25% вероятность угадать ответ, наобум поставив крестик.
Неплохим инструментом для изучения влияния закрытых вопросов на результаты ЕГЭ является схема Бернулли, позволяющая рассчитывать вероятность получения определенного результата в серии независимых испытаний. В нашем случае мы имеем серию из n заданий части А, в каждом из них есть 4 альтернативы ответа. Угадывание наступает с вероятностью 0,25 (при трех альтернативах — 0,33) и ошибка с вероятностью 0,75 (0,66).
В соответствии с формулой Бернулли
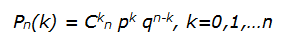
где Рn(k) есть вероятность того, что в n испытаниях произойдет ровно k успехов, определяем, с какой вероятностью можно получить определенное число баллов путем угадывания в серии из n испытаний при начислении 1 балла за верный ответ. Процент вероятности получения определенного результата путем гадания приведен в таблице 1.
Таблица 1.
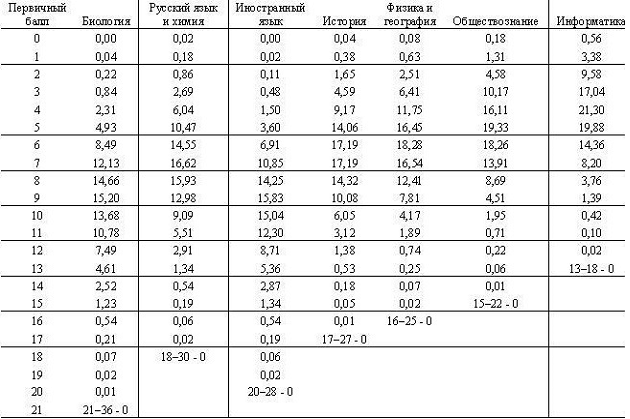
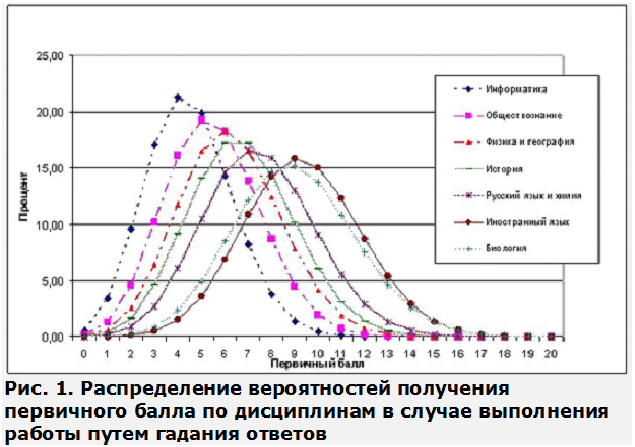
Проиллюстрируем таблицу 1 графиком, который показывает как по мере увеличения в работе числа закрытых вопросов от наименьшего (информатика) к наибольшему (биология) растут шансы учащихся получить баллы. Результаты по иностранным языкам несколько отличаются из-за того, что вопросы здесь закрыты тремя альтернативами. Соответственно таблица результативности выполнения заданий части А путем гадания будет выглядеть следующим образом (рис.1 и табл.2):
Таблица 2.
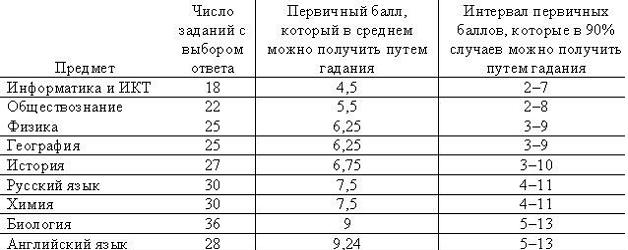
Подсчеты по схеме Бернулли показывают, что ноль баллов на ЕГЭ получить почти невозможно. Для этого нужно сдать работу пустой. И действительно, школьники по всем предметам ноль баллов получают чаще, чем один-три балла. Происходит это, потому что они сдают пустые работы.
Следы закрытых вопросов в виде «горбов» в начале шкалы хорошо видны в распределении учащихся по баллам на обязательных экзаменах. Наиболее ярко это проявилось в период, когда охват испытаниями стал почти 100% и действовала норма, позволявшая в любом случае получить удовлетворительную оценку. Зная, что тройка им гарантирована, выпускники наобум проставляли крестики в бланке ответов и сдавали работы. Например, в 2007–2008 годах на ЕГЭ по математике почти каждый пятый школьник страны выполнял задания «методом тыка». На графике выбросы значений, соответствующие результативности простого гадания ответов, обведены кружком (рис.2). В ежегодных отчетах Федерального института педагогических измерений (ФИПИ) знания детей, показавших минимальный их уровень, постоянно характеризовались как отрывочные и бессистемные. Хотя какая уж тут система?
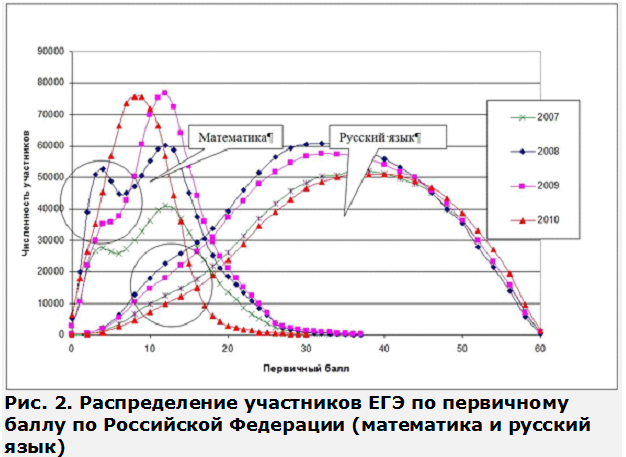
Столь явное проявление в математике заданий-угадаек, выражающееся в распаде массива участников на две части, объясняется тем, что форма записи ответа (числа, выражения, числовые множества, уравнения) не позволяла выбирать альтернативы методом исключения неправдоподобного. Это стимулировало формальное отношение к выполнению работы: учащиеся стали наобум отмечать варианты ответов. В распределении по русскому языку, КИМы которого почти наполовину состоят из вопросов с альтернативами, содержащих подсказки, подъем линии графика той же природы сдвинут вправо и выражен менее (рис.2).
На графиках прочих предметов всплесков, соответствующих результативности гадания, мы не найдём. (Впрочем, если заставить выпускников сдавать все экзамены, вопросы-угадайки встанут «горбами» в начале шкалы по всем предметам аналогично тому, как это было в распределении по математике.) На экзаменах по выбору дети стараются максимально хорошо выполнить работу и к гаданию не прибегают. Однако следы вопросов-угадаек мы обнаружим и тут. Обратим внимание, что по всей стране и всем дисциплинам учащихся с 4–5 и менее первичными баллами практически нет. Чем больше в работе закрытых вопросов, тем выше вероятность что-то угадать, тем меньше вероятность получения низких результатов. Как только школьник начинает, даже глядя в потолок, заполнять бланк он непременно проставит верные ответы и что-то «заработает». График распределения по баллам хорошо иллюстрирует этот факт (рис.3).
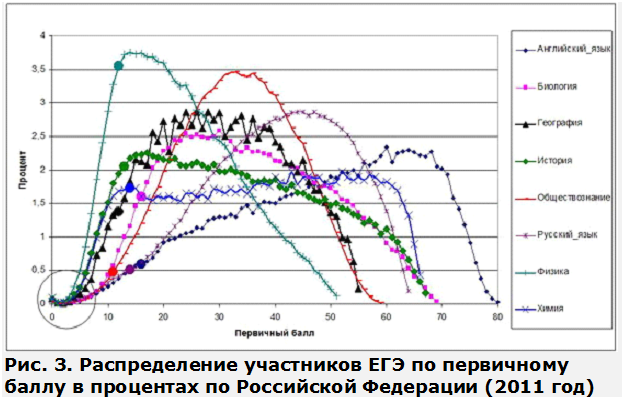
Понимание того, что знания выпускников проверяются с помощью закрытых вопросов, в значительной мере определяющих результаты испытаний, позволяет избежать ошибок толкования последних. Так, например, уровень, обозначенный Рособрнадзором как минимальный, в значительной мере достигается элементарным гаданием ответов. Поэтому при интерпретации итогов ЕГЭ точку отсчета результативности учащихся следует считать не с нуля, а от значения, когда вероятность получить высокие баллы, наобум отмечая варианты, становится допустимо малой (менее 1%). Для русского языка, например, она составляет 14 баллов, что хорошо согласуется с границей минимального уровня усвоения курса, которую ежегодно устанавливает Рособрнадзор — 17 баллов (2013г.). Для английского языка эти показатели насчитывают 16 баллов по формуле Бернулли (16 — Рособрнадзор), биологии — 17 (16), географии — 12 (14), истории — 13 (13), обществознания — 14 (15), физики — 12 (12), химии — 14 (14). (На графике соответствующие точки обозначены маркером). Данный факт свидетельствует, насколько невысоки федеральные требования к подготовке учащихся. Ведь работу нужно выполнить немногим лучше, чем с известной долей везения наугад проставлять крестики в бланке ответов.
Проблема вопросов-угадаек уже поднималась во время работы Комиссии по совершенствованию ЕГЭ, созданной при Президенте РФ. В декабре 2010 года на встрече с президентом министр образования заверил, что его ведомство неоднократно проводило исследования, доказывающие невозможность сдать ЕГЭ путем угадывания. Более того, из КИМов по математике закрытые вопросы вообще исключены. Все это действительно так. Обратим, однако, внимание на одну деталь: убраны закрытые вопросы из контрольно-измерительных материалов дисциплины, где они были представлены менее всего. В 2009 году (до смены формата экзамена) их доля в первичном балле за всю работу составляла лишь 27% (для сравнения: в русском языке, биологии, физике, химии их около 50%). На наш взгляд, часть А из КИМов по математике удалена не столько потому, что ее легко заменить открытыми вопросами с ответами в виде целого числа или десятичной дроби, хорошо читаемых машиной (ведь в физике и информатике часть А осталась), сколько потому, что распределение результатов наглядно и «предательски» показывало, как велико влияние закрытых вопросов на общий результат.
Казалось бы, стоит ли обращать внимание на такую мелочь, как возможность школьника что-то угадать? Таким путем высоких результатов на экзамене никогда не получить. К тому же все равно все участники ЕГЭ находятся в одинаковых условиях.
Посмотрим, тем не менее, к чему такое допущение приводит на практике. Сравнение достижений учащихся производится не по первичным, а по тестовым баллам, система начисления которых равных условий уже не создает. Шкалы перевода предусматривают начисление максимальных тестовых баллов минимальным и максимальным первичным. В результате участники, проставляющие на экзамене кресты «от фонаря», тестовыми баллами МАКСИМАЛЬНО НАГРАЖДАЮТСЯ. Но это полбеды. Учащиеся, делающие лишь единичные ошибки, потерей тестовых баллов МАКСИМАЛЬНО НАКАЗЫВАЮТСЯ.
Например, за работу наугад на экзамене по русскому языку «непредвзятая диагностика ЕГЭ» одарит лоботряса 7–8 первичными или 15–17 тестовыми баллами. Сильных школьников, потерявших 7–8 первичных баллов из 80 возможных (10%), она обворует на пятую часть тестовых (20%). Отсюда понятной становится уже почти закономерная картина: неожиданно высокие результаты у детей, учившихся в школе на «3–4», и относительно низкие показатели у отличников, призеров олимпиад и различных конкурсов по предметам. Именно нелепая система оценивания позволяет обвинять школы в «липовых» медалистах, а олимпиады и конкурсы — в слабых победителях. Собственно в этом кривом зеркале ЕГЭ и отражается состояние школьной подготовки.
Отказ от закрытых вопросов и линейная шкала перевода баллов сделают систему оценивания более корректной. Основной причиной сохранения закрытых вопросов является технологичность их обработки. Между тем открытые вопросы тоже легко и быстро обрабатываются. Следует лишь изменить технологию: перейти от проверки символов, которыми записан ответ, к проверке его смысла. В действующей практике каждый бланк ответов верификаторы до рези в глазах, «до буквы», сравнивают с текстом, полученным при машинном распознавании. Таким способом открытые вопросы действительно проверяются очень трудно.
На наш взгляд следует поступать иначе. Необходимо перевести результаты распознавания задания (пусть это будет, скажем, В1) в массив и отсортировать его по алфавиту (или по той или иной степени сходства). Поскольку ответы представляют собой однотипные записи с вариациями, вызванными ошибками распознавания, сходные ответы тут же сгруппируются. В группах сразу будут видны отклонения в орфографии отдельных записей, не влияющие на их смысл. Ошибки исправляются приведением ответов к единой для группы форме одним щелчком мыши. И так с каждой группой. После этого массив будет представлять собой несколько групп грамматически верных и одинаковых записей, соответствующих смыслу, который вкладывал школьник. Ответы, не попавшие в группы, будут единичны. Их легко просмотреть обычным способом. Аналогично далее проверяется задание В2 и т.д. Такая проверка может быть сделана очень быстро и качественно. Осталось лишь соотнести полученные варианты с верным ответом.
Применение архаичной системы проверки работ является причиной многих «болячек» экзамена. Так, например, удаление из контрольно-измерительных материалов по математике заданий в закрытой форме без адекватных изменений в технологии верификации повлекло обеднение содержательной части проверяемых элементов базового уровня. В угоду технологичности обработки результатов (ответ должен быть записан числом, легко читаемым машиной) были принесены в жертву такие вопросы курса алгебры и начала анализа средней школы базового уровня как множество значений функции, графики основных элементарных функций, правила дифференцирования и таблица производных. Не проверяется теперь на базовом уровне и такой блок раздела «Уравнения и неравенства» как задачи на нахождение множества решений неравенств (дробно-линейного, показательного, логарифмического, иррационального). Задание В12 в некоторых вариантах только на первый взгляд требует решения неравенства. На самом деле в этих задачах достаточно найти корни соответствующего уравнения. В итоге умение решать неравенства (и их системы) проверяются только в заданиях повышенного (С3) или высокого (С5) уровня. По этой же причине не проверяются и умения решать тригонометрические уравнения. Более того, ограничения на форму записи ответа (целое число или конечная десятичная дробь) содержит обычную для закрытых вопросов подсказку в случае, если в результате вычислений, например, получается рациональное число ⅓, которое нельзя представить в виде конечной десятичной дроби.
Наглядный пример влияния формы записи ответа на результат представляет собой задание типа: «Найдите наименьшее значение функции
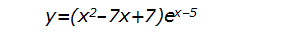
на отрезке[4,6]». Очевидно, что только при х=5 можно получить ответ, который не содержит числа е, а значит и решать эту задачу нет смысла, благодаря ограничениям на запись ответа.
(продолжение следует)